Создание высокотехнологичных конкурентоспособных технических систем в настоящее время является наиважнейшей задачей всех без исключения технических отраслей промышленности России. Сложная экономическая и политическая ситуация требует от предприятий, и прежде всего оборонных отраслей промышленности, искать подходы для повышения конкурентоспособности сложных технических систем (СТС) как на внешнем, так и на внутреннем рынках. При этом конкурентоспособность СТС определяется уровнем не только ее экономических, технических и эксплуатационных параметров, которые позволяют выдержать соперничество (конкуренцию) с другими аналогичными системами на рынке, но и послепродажного обслуживания, возможностью поддержания заданных эксплуатационно-технических характеристик минимальными средствами.

Одним из важнейших этапов эксплуатации СТС являются мероприятия, связанные с поддержанием их работоспособного состояния. К таким мероприятиям, в первую очередь, относятся техническое обслуживание и текущий ремонт. Основная задача технического обслуживания – предупредить нарушение работоспособного состояния СТС, задача текущего ремонта – оперативно восстанавливать работоспособное состояние. При решении этих задач важную роль играет система контроля технического состояния (КТС) СТС.

Если СТС является высокоответственным изделием, что присуще образцам вооружения, атомной, энергетической промышленности и т.д., то вопросы предотвращения аварийных ситуаций, связанных
с нарушением работоспособности изделий, имеют первостепенной значение. 

Для высокотехнологичных образцов в этих условиях необходимо развивать более совершенную
систему КТС, которая должна получать не только мгновенные значения параметров, характеризующих работоспособность образца, но и осуществлять прогноз их деградации с целью дальнейшего профилактического обслуживания (технического обслуживания либо профилактического ремонта).

Система КТС образца должна строиться на основе существующих автоматических (автоматизированных) систем функционального контроля (АФК) с интегрированным алгоритмом прогнозирования параметров. Предлагается рассмотреть механизм работы универсального алгоритма прогнозирования технического состояния, основанного на использовании теории самоорганизации [1]. 

Алгоритм по данным о значениях параметров, определяющих работоспособность образцов, позволяет построить тренды этих параметров и оценить их изменение в границах установленных допусков с целью дальнейшего определения времени перехода образца в неработоспособное состояние.

В качестве исходных данных при моделировании изменения технического состояния образца вооружения и военной техники используются измеренные в ходе проведения АФК значения параметров. Наличие информации о значениях параметра xi в различные моменты времени позволяет получить для каждого параметра динамический ряд xt (t = 1, …, n).  

Далее на точках динамического ряда необходимо построить математическую модель изменения значений параметра. В основе большинства методов построения математических моделей поведения параметров технических систем лежит множественный регрессионный анализ. Суть его в том, что на основе наблюдаемых значений параметра в определенные моменты времени

                                        (1)

где Тнабл. – интервал времени наблюдения за поведением параметра, строятся регрессионные зависимости на всем интервале их изменения во времени в виде полиномов различной степени:

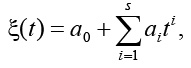                                                                           (2)

где ai – коэффициенты полинома; s – показатель степени полинома.

В этом случае задача заключается в нахождении числовых значений коэффициентов регрессионной модели по одному из известных методов (например, по методу наименьших квадратов). При выборе регрессионной модели наиболее сложным является определение степени полинома, который не только наиболее адекватно описывал бы имеющуюся тенденцию, но и обладал бы наилучшими прогнозными свойствами.

При выборе степени полинома (2) наиболее предпочтительным является метод группового учета аргументов (МГУА) [2–4]. Этот метод достаточно хорошо зарекомендовал себя в различных областях науки: распознавание образов, нахождение физических и нефизических закономерностей, идентификация нелинейных систем, краткосрочное и долгосрочное прогнозирование стационарных и нестационарных процессов, управление сложными техническими объектами и др. [5]. Основная идея МГУА состоит в утверждении, что для задачи однократного прогноза целесообразно несколько снизить точность определения оценки коэффициентов уравнения регрессии, но за счет этого придать ему большую регулярность (прогнозирующую силу). Целью при этом является не минимум ошибки на уже известных точках интерполяции, а минимум ошибки на новых точках, которыми в момент синтеза уравнения регрессии пока еще нет.

Рассмотрим моделирование изменения технического состояния j-го устройства. Пусть имеется выборка измеренных в процессе АФК значений параметров устройства в виде динамического ряда (1), на основе которой необходимо определить, как будет осуществляться деградация параметра во времени и когда наступит момент нарушения работоспособности. На этой выборке строятся несколько уравнений регрессий, аппроксимирующих тренд в виде полиномов с постепенно увеличивающимся показателем степени. Необходимо путем перебора выбрать уравнение оптимальной сложности для решения задачи прогнозирования. Для этого точки последовательности N0 статистических данных о результатах измерения значений параметра разбиваются на две подвыборки: обучающую c числом точек Nоб и проверочную c числом точек Nпр. Чтобы провести такое разделение, у имеющейся статистической выборки данных находим среднее значение:

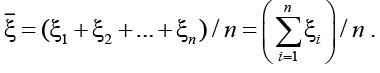                                     (3)

Затем необходимо все точки последовательности N0 ранжировать, то есть расположить в ряд по величине дисперсии D:

.                                                                               (4)

Все точки, наиболее удаленные от среднего значения, помещаются в обучающую последовательность, остальные – в проверочную. Это позволяет уменьшить ошибки в определении коэффициентов
регрессии. При этом экспериментально установлено, что отношение числа точек в обучающей последовательности к числу точек в проверочной имеет оптимальное значение , а минимально необходимое число точек для проведения расчетов равно 5 (4 точки в обучающую последовательность, 1 – в проверочную) [2].

Следующим этапом является построение на точках обучающей последовательности множества всевозможных уравнений тренда при их постепенном усложнении.

Далее на проверочной последовательности находится рассогласование (разность реальных и прогнозных значений) для каждой реализации процесса изменения параметра (для каждой функции, аппроксимирующей тренд):

,                                                                    (5)

где  – значение прогноза в i-й точке, i=1, 2, 3, …, Nпр по проверочной модели для каждой функции, построенной на обучающей последовательности;  – действительное значение в той же точке.

Затем производится расчет величины среднеквадратической ошибки рассогласования в соответствии с выражениями:

                                                   (6)

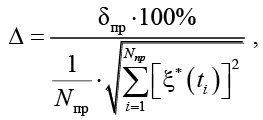                                                          (7)

где δпр – абсолютное значение величины среднеквадратической ошибки рассогласования; ∆ – относительное значение величины ошибки.

По критерию ∆®min выбираются полиномиальные зависимости с таким показателем степени, при котором имеют место минимальные ошибки рассогласования прогнозных и действительных значений полиномиальных функций, построенных на обучающей последовательности. Необходимость в отборе нескольких полиномиальных зависимостей вызвана тем, что критерий D имеет полимодальный характер, что может привести к выбору зависимости, не обладающей лучшими прогнозными свойствами. Устранение этой неоднозначности возможно путем введения еще одного дополнительного критерия – критерия несмещенности, который имеет унимодальный характер и позволяет выбрать единственную оптимальную зависимость. Для этого вся последовательность точек вновь делится на две последовательности А и В таким образом, чтобы АÇВ = Æ и АÈВ = N0. Далее для каждой зависимости производится пересчет коэффициентов по методу наименьших квадратов на точках обучающей последовательности. По критерию минимума смещения

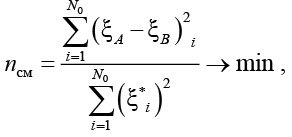                                                     (8)

где xА – выходная величина полиномиальной зависимости, оценки коэффициентов которой получены на подвыборке А; xВ – выходная величина полиномиальной зависимости, оценки коэффициентов которой получены на подвыборке В; выбирается единственная аппроксимирующая зависимость, обладающая наилучшими прогнозными свойствами.

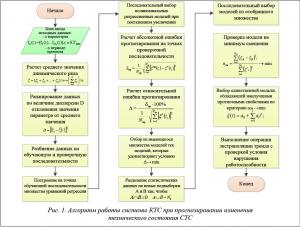
В результате получаем реализацию процесса изменения параметра устройства вида (2). Алгоритм работы системы КТС при прогнозировании изменения технического состояния СТС приведен на рисунке 1.

Таким образом, полученный алгоритм позволяет по значениям контролируемых параметров, определяющих работоспособность устройств СТС, оценить изменение ее технического состояния за определенный период. Проведение подобных процедур с множеством параметров, характеризующих работоспособность СТС, позволит определить объемы и сроки проведения технического обслуживания.

Для этого необходимо провести операцию экстраполяции тренда. Операцию экстраполяции можно представить в виде определения значения функции

                                                   (9)

где x(t + ТПР) – экстраполируемое значение функции; ТПР – период прогноза.

При этом проверяется условие работоспособности по данному параметру:

                                                                 (10)

где xiн и (или) xiв – соответственно нижнее и верхнее предельно допустимые значения i-го параметра.

Выбор периода прогноза может осуществляться итерационно через последовательное задание значений периода контроля с проверкой условия (10) или на величину ожидаемого начала и продолжительности практического использования СТС. При этом можно определить ожидаемый объем регламентных работ на момент начала использования по назначению и техническое состояние на период этого использования.

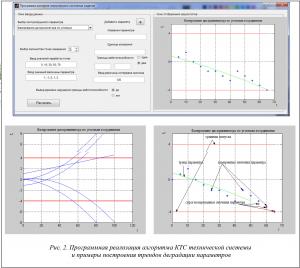
Реализация данного алгоритма в среде MATLAB и апробация на реальных технических системах военного назначения показали достаточно высокую практическую применимость программы [6]. На рисунке 2 представлены графический интерфейс программы и примеры построения отдельных реализаций параметров.

Разработанная программа позволяет отображать как фактические, так и прогнозируемые значения параметров для различных периодов прогноза, модели этих параметров в виде трендов полиномов оптимальной сложности относительно границ работоспособности и номинального значения. Кроме этого,

имеется возможность получения статистической выборки трендов параметров для определения закона распределения и его характеристик путем запоминания моделей как от измерения к измерению, так и оперированием всей историей целиком.

Таким образом, совершенствование систем КТС в направлении внедрения алгоритмов прогнозирования позволит в условиях временных и технологических ограничений отыскать рациональные способы поддержания заданного уровня эксплуатационно-технических характеристик СТС.

Литература

1. Ивахненко А.Г., Зайченко Ю.П., Димитров В.Д. Принятие решений на основе самоорганизации. М.: Сов. радио, 1976. 280 с.

2. Ивахненко А.Г., Юрачковский Ю.П. Моделирование сложных систем по экспериментальным данным. М.: Радио и связь, 1987. 120 с.

3. Степашко В.С., Костенко Ю.В. Исследование свойств комбинаторно-селекционного (многоэтапного) алгоритма МГУА // Моделирование и управление состоянием эколого-экономических систем региона: сб. науч. тр. К.: Изд-во ИК НАНУ, 2001. С. 69–76.

4. Зайченко Ю.П., Заец И.О., Камоцкий О.В. [и др.]. Исследование разных видов функций принадлежности параметров нечетких прогнозирующих моделей в нечетком методе группового учета аргументов. УСиМ. 2003. № 2. С. 56–67.

5. GMDH. URL: http:/www.gmdh.net (дата обращения: 3.04.2017).

6. Брежнев Д.Ю., Овруцкий Д.А., Брежнев Е.Ю., Нестерчук И.В. Программа оценки изменения параметров технического состояния образца ВВТ и прогноза их деградации. Свид. о регистр. прогр. для ЭВМ № 2017614166. Опубл. 06.04.2017.