Автоматическая трехмерная реконструкция сцен окружающего мира по набору изображений является одной из классических задач компьютерного зрения и графики. Трехмерные модели находят свое применение в системах виртуальной и дополненной реальности, в робототехнике, медицине, геоинформационных системах и ряде других областей. При этом одним из ключевых шагов реконструкции является восстановление облака трехмерных точек, по которым потом строится полигональная трехмерная модель.
Существует множество подходов к извлечению трехмерной информации из множества изображений сцены. Однако часть из них, например методы реконструкции по фокусировке (две группы методов, известные в англоязычной литературе как shape from focus и shape from defocus), накладывают серьезные ограничения на изображения и условия съемки. Другие, например алгоритмы реконструкции по закраске (от англ. shape from shading), подразумевают наличие на входе лишь единственного изображения [1]. В случае же больших неупорядоченных наборов изображений, полученных при неконтролируемых условиях съемки, традиционным подходом является реконструкция на основе стереоскопической информации (shape from stereo), или стереореконструкция.
Стереореконструкция называется плотной, если для каждой точки изображения восстанавливается соответствующая трехмерная точка. В противном случае стереореконструкцию называют разреженной. В контексте общей задачи трехмерной реконструкции наибольший интерес представляет именно плотная стереореконструкция, поскольку она позволяет наиболее полно использовать представленную на изображениях информацию.
Несмотря на то, что принято разделять задачи плотной стереореконструкции по множеству изображений (multiview stereo) и по паре изображений (binocular stereo), зачастую первая из них сводится ко второй: сначала выполняется плотная стереореконструкция для каждой пары перекрывающихся снимков, после чего результаты объединяются. Поэтому в рамках данной статьи рассматривается именно вторая задача.
Постановка задачи
Целью задачи плотной стереореконструкции по паре изображений является вычисление трехмерных координат каждой точки сцены, запечатленной на данных изображениях. Параметры внутренней и внешней калибровки камер для каждого из снимков считаются известными. Отметим, что в разных практических задачах это может быть реализовано по-разному. Например, внутренние параметры камеры могут быть вычислены заранее с помощью процедуры калибровки камеры, а положение и ориентация могут считываться с датчиков систем глобального позиционирования (GPS, ГЛОНАСС) и инерциальных навигационных систем (INS – Inertial Navigation System). Если же эта информация недоступна, а предварительная калибровка невозможна либо используются произвольные снимки из Сети, полученные с разных камер, то параметры внутренней и внешней калибровки могут быть вычислены в результате предварительного сопоставления изображений и применения процедуры глобального уравнивания параметров. Так или иначе, с точки зрения задачи плотной стереореконструкции способ их вычисления не имеет значения.
Процесс восстановления облака трехмерных точек по паре изображений сцены можно представить в виде следующих трех шагов:
- ректификация изображений;
- плотное сопоставление ректифицированных изображений;
- реконструкция облака трехмерных точек.
Рассмотрим каждый шаг подробнее. Как известно, каждой точке на одном из двух изображений сцены соответствует прямая на втором изображении, называемая эпиполярной линией [2]. При известных параметрах калибровки камер преобразование из точки в прямую известно и задано однозначно. А значит, область поиска соответствия для каждой точки можно ограничить лишь отвечающей ей эпиполярной линией на другом изображении. Более того, можно установить взаимно-однозначное соответствие между эпиполярными линиями на двух изображениях (рис. 1).
Для технического упрощения подобного одномерного поиска на практике используют специальное представление изображения, при котором его эпиполярные линии совпадают со строками пикселей. Такое изображение называется ректифицированным, а процесс его получения ректификацией. Обычно ректификация пары изображений заключается в их проецировании на некоторую плоскость, параллельную стереобазе (стереобазой двух снимков называют отрезок, соединяющий их оптические центры).
Пусть IL и IR – соответственно левое и правое ректифицированные изображения сцены. Тогда для любой пары соответствующих точек p1ÎIL, p2ÎIR верно утверждение 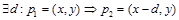 . Величина смещения d называется диспаритетом (disparity) в точке p1 (в русскоязычной литературе, посвященной зрительной системе человека, данное понятие принято называть диспаратностью) (disparatus). Таким образом, соответствие между каждой парой точек определяется величиной диспаритета. Матрица D, каждый элемент которой содержит диспаритет соответствующего пикселя изображения I, называется картой диспаритета для изображения I. Как правило, используют представление карты диспаритета в виде полутонового изображения, яркость каждого пикселя которого кодирует величину диспаритета в данной точке. На рисунке 2 приведен пример пары ректифицированных изображений и карты диспаритета, соответствующей левому изображению. Отметим, что минимальное и максимальное значения диспаритета dmin, dmax обычно считаются заданными заранее.
. Величина смещения d называется диспаритетом (disparity) в точке p1 (в русскоязычной литературе, посвященной зрительной системе человека, данное понятие принято называть диспаратностью) (disparatus). Таким образом, соответствие между каждой парой точек определяется величиной диспаритета. Матрица D, каждый элемент которой содержит диспаритет соответствующего пикселя изображения I, называется картой диспаритета для изображения I. Как правило, используют представление карты диспаритета в виде полутонового изображения, яркость каждого пикселя которого кодирует величину диспаритета в данной точке. На рисунке 2 приведен пример пары ректифицированных изображений и карты диспаритета, соответствующей левому изображению. Отметим, что минимальное и максимальное значения диспаритета dmin, dmax обычно считаются заданными заранее.
 При известных параметрах калибровки камер диспаритет произвольной точки может быть преобразован в ее глубину, то есть удаленность от плоскости изображения. Глубина точки обратно пропорциональна величине диспаритета в ней. Для наглядной демонстрации данной взаимосвязи можно провести параллель со зрительной системой человека: чем ближе к нам находится наблюдаемая точка, тем больше ее смещение между изображениями, получаемыми левым и правым глазом. Таким образом, по карте диспаритета может быть восстановлено плотное облако трехмерных точек сцены.
При известных параметрах калибровки камер диспаритет произвольной точки может быть преобразован в ее глубину, то есть удаленность от плоскости изображения. Глубина точки обратно пропорциональна величине диспаритета в ней. Для наглядной демонстрации данной взаимосвязи можно провести параллель со зрительной системой человека: чем ближе к нам находится наблюдаемая точка, тем больше ее смещение между изображениями, получаемыми левым и правым глазом. Таким образом, по карте диспаритета может быть восстановлено плотное облако трехмерных точек сцены.
Важно отметить, что первый и третий из описанных шагов, то есть ректификация изображений и реконструкция облака трехмерных точек, являются давно решенными и не представляющими научного интереса техническими задачами. Вся сложность задачи плотной стереореконструкции заключается во втором шаге – вычислении карты диспаритета для пары ректифицированных изображений. Поэтому далее в данной статье под плотной стереореконструкцией по паре изображений будет пониматься только вычисление карты диспаритета, а исходные изображения всегда будут считаться ректифицированными. Задачу плотной стереореконструкции по паре изображений будем также сокращенно называть задачей плотного стерео.
Обзор алгоритмов плотной стереореконструкции по паре изображений
Основные понятия и определения. Будем ориентироваться на общепринятую терминологию и таксономию, предложенные в 2001 году в работе [3], и введем ряд понятий и определений.
Пару исходных ректифицированных изображений будем обозначать IL, IR, а соответствующие им карты диспаритета DL, DR. Для решения задачи достаточно найти одну из карт DL, DR. Исходные изображения будем считать полутоновыми. Как показывают проведенные исследования [4], информация о цвете не способствует улучшению результатов алгоритмов плотного стерео, поэтому подавляющее большинство методов, в том числе и предлагаемый автором, используют полутоновое представление исходных изображений.
Стоимостью Cp(d) присвоения диспаритета d точке p, или стоимостью сопоставления (matching cost), называется численная величина, представляющая собой штраф за определенное значение диспаритета в данной точке. Пусть p=(x, y)ÎIL, тогда простейшим примером стоимости может служить абсолютная величина разности яркостей соответствующих пикселей 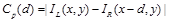 .
.
Агрегированной стоимостью Ap(d) присвоения диспаритета d точке p называется стоимость, оцененная по некоторой области W, являющейся, как правило, окрестностью точки p. Например, часто используется простая сумма стоимостей в каждой точке области: 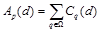 . Процесс вычисления агрегированной стоимости по заданной области называется агрегацией стоимости по данной области, или просто агрегацией.
. Процесс вычисления агрегированной стоимости по заданной области называется агрегацией стоимости по данной области, или просто агрегацией.
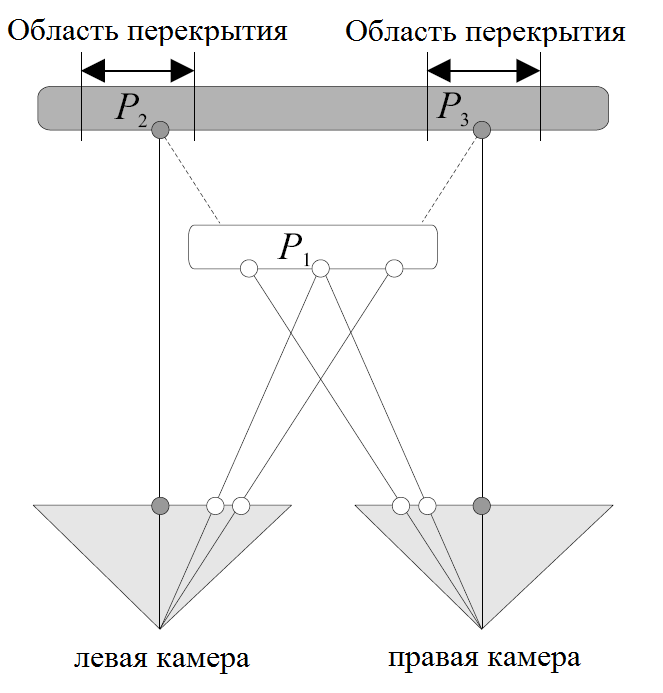
Другим важным понятием является понятие загороженности. Точка 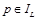 называется загороженной, или перекрытой, если для нее не существует правильного соответствия на изображении IR. Причина возникновения подобных точек в смещении объектов переднего плана между двумя изображениями, ввиду чего близкая к границе такого объекта точка может быть видна на одном изображении, но загорожена объектом на другом (рис. 3). Связанное множество (сегмент) загороженных точек будем называть областью перекрытия. Поскольку для загороженных точек не существует соответствия, восстановление правильных значений диспаритета в них является одной из основных трудностей задачи плотного стерео.
называется загороженной, или перекрытой, если для нее не существует правильного соответствия на изображении IR. Причина возникновения подобных точек в смещении объектов переднего плана между двумя изображениями, ввиду чего близкая к границе такого объекта точка может быть видна на одном изображении, но загорожена объектом на другом (рис. 3). Связанное множество (сегмент) загороженных точек будем называть областью перекрытия. Поскольку для загороженных точек не существует соответствия, восстановление правильных значений диспаритета в них является одной из основных трудностей задачи плотного стерео.
 Локальные методы. Простейший наивный подход – найти для каждого пикселя левого изображения ближайший по цвету пиксель в соответствующей строке правого изображения – очевидно, дает неприемлемый результат, поскольку надежно различить точки только на основании их яркости невозможно. Поэтому требуется учет яркости других пикселей. Локальные методы используют для вычисления диспаритета в каждой точке информацию лишь с части пикселей изображения, как правило, из окрестности данной точки. В качестве окрестности обычно выбирается квадратная или прямоугольная область вокруг заданной точки, называемая окном. Стоимость Cp(d) присвоения точке p диспаритета d, как правило, принимается равной разности яркости соответствующих пикселей. Часто применяется и метрика из работы [5], в которой для уменьшения влияния эффектов дискретизации изображения в каждой точке проверяется несколько интерполированных значений яркости. Агрегированная по окну W стоимость, как правило, берется равной сумме стоимостей в каждой точке окна:
Локальные методы. Простейший наивный подход – найти для каждого пикселя левого изображения ближайший по цвету пиксель в соответствующей строке правого изображения – очевидно, дает неприемлемый результат, поскольку надежно различить точки только на основании их яркости невозможно. Поэтому требуется учет яркости других пикселей. Локальные методы используют для вычисления диспаритета в каждой точке информацию лишь с части пикселей изображения, как правило, из окрестности данной точки. В качестве окрестности обычно выбирается квадратная или прямоугольная область вокруг заданной точки, называемая окном. Стоимость Cp(d) присвоения точке p диспаритета d, как правило, принимается равной разности яркости соответствующих пикселей. Часто применяется и метрика из работы [5], в которой для уменьшения влияния эффектов дискретизации изображения в каждой точке проверяется несколько интерполированных значений яркости. Агрегированная по окну W стоимость, как правило, берется равной сумме стоимостей в каждой точке окна: 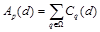 . В качестве решения в точке p выбирается диспаритет, дающий наименьшую агрегированную стоимость:
. В качестве решения в точке p выбирается диспаритет, дающий наименьшую агрегированную стоимость: 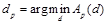 (здесь и далее значение диспаритета в точке p будем обозначать dp).
(здесь и далее значение диспаритета в точке p будем обозначать dp).
Достоинством локальных алгоритмов является скорость работы. С помощью оптимизационной техники, известной как скользящее окно (sliding window), сложность вычислений можно сделать независимой от размера окна W [6] и линейно зависимой от величины диапазона диспаритетов 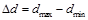 . Однако их существенным недостатком является неявное предположение о постоянном диспаритете внутри окна, которое, очевидно, нарушается в большинстве случаев. Развитие локальных алгоритмов в последние годы идет по пути устранения этого недостатка.
. Однако их существенным недостатком является неявное предположение о постоянном диспаритете внутри окна, которое, очевидно, нарушается в большинстве случаев. Развитие локальных алгоритмов в последние годы идет по пути устранения этого недостатка.
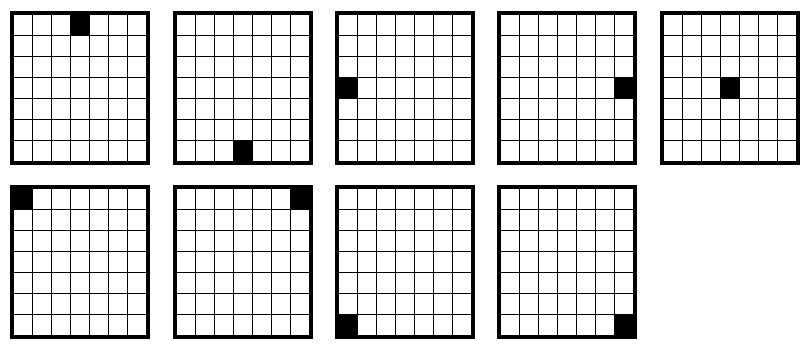
Одним из способов обойти проблему постоянного диспаритета является варьирование формы и структуры окна, использование адаптивных окон. Например, в работе [7] авторы предлагают использовать 9 различных окон одинакового размера (рис. 4), предполагая, что хотя бы одно из них не попадет на область разрыва диспаритета (резкое изменение значения диспаритета характерно для границ между объектами заднего и переднего плана). Итоговая стоимость сопоставления для пикселя определяется как минимум стоимостей, агрегированных по каждому из окон. Похожий подход предложен в [8]: окно разбивается на несколько более мелких окон, и в агрегации участвуют только те окна, которые дают меньшую стоимость.
Другой подход заключается в использовании окон с адаптивными весами. Вклад каждого пикселя внутри окна в общую агрегированную стоимость взвешивается с некоторым коэффициентом. В идеальном случае в агрегации должны участвовать только точки с одинаковым диспаритетом. Поэтому коэффициент в точке q делают пропорциональным вероятности того, что данная точка имеет тот же диспаритет, что и точка p, для которой ищется решение. Конкретный способ вычисления этого коэффициента варьируется от алгоритма к алгоритму, однако можно выделить три основных учитываемых фактора (рис. 5):
-
 цветовое сходство;
цветовое сходство; - близость по расстоянию;
- наличие разделяющей цветовой границы между точками.
Формула вычисления весов, комбинирующая первые два признака – цвет и расстояние, приведена в работе [9]. В статье [10] авторы используют третий признак – наличие границы. Они рассматривают все пути, связывающие две точки, и определяют вес как функцию, обратно пропорциональную стоимости наилучшего пути. Стоимость пути характеризуется перепадами яркости вдоль этого пути: чем больше перепады, тем выше стоимость. Таким образом, если две точки лежат по разные стороны от границы между объектами, любой путь между ними будет иметь большую стоимость и вес будет маленьким.
Важно отметить, что качество, достигаемое сегодня локальными алгоритмами с адаптивными весами, является наивысшим среди всех локальных методов и сравнимо с качеством глобальных алгоритмов. Однако для окон с адаптивными весами невозможно применение техники скользящего окна, поэтому основанные на них алгоритмы работают заметно дольше, чем прочие локальные методы. Другим их недостатком является проблема выбора размера окна. С одной стороны, окно должно быть большим, чтобы захватывать достаточное количество текстуры, что особенно актуально для слабо текстурированных областей изображений. С другой стороны, большие окна портят мелкие детали, размывают края объектов и вызывают известный эффект раздувания объектов переднего плана (foreground fattening).
Глобальные методы формулируют вычисление карты диспаритета как задачу разметки связного графа G=(V, E), вершины V которого соответствуют пикселям изображения. Каждой вершине pÎV присваивается метка 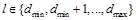 , обозначающая величину диспаритета в данном пикселе. Алгоритмы данной группы стремятся найти такую карту диспаритета D, которая минимизирует заданный функционал энергии. Таким образом, решение не ищется независимо в каждой точке, а каждый пиксель изображения оказывает влияние на решение во всех остальных пикселях – отсюда и название данной группы методов. В минимальном варианте оптимизируемый функционал представляет собой сумму двух слагаемых, называемых также потенциалами:
, обозначающая величину диспаритета в данном пикселе. Алгоритмы данной группы стремятся найти такую карту диспаритета D, которая минимизирует заданный функционал энергии. Таким образом, решение не ищется независимо в каждой точке, а каждый пиксель изображения оказывает влияние на решение во всех остальных пикселях – отсюда и название данной группы методов. В минимальном варианте оптимизируемый функционал представляет собой сумму двух слагаемых, называемых также потенциалами:
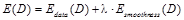 . (1)
. (1)
Унарный потенциал (data term) 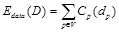 отвечает за согласованность решения в каждой точке p по цвету. Парный потенциал (smoothness term)
отвечает за согласованность решения в каждой точке p по цвету. Парный потенциал (smoothness term) 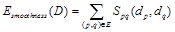 реализует предположение о гладкости решения, штрафуя за резкие разрывы диспаритета. При этом обычно поощряется наложение областей разрыва диспаритета на границы яркости на изображении – величина штрафа в таком случае меньше.
реализует предположение о гладкости решения, штрафуя за резкие разрывы диспаритета. При этом обычно поощряется наложение областей разрыва диспаритета на границы яркости на изображении – величина штрафа в таком случае меньше.
Все глобальные алгоритмы можно охарактеризовать по следующим критериям.
- Вид функционала энергии. Идеальный функционал должен быть таким, чтобы его значение достигало глобального минимума на эталонных данных. Однако это условие на сегодняшний день не выполняется [11].
- Алгоритм минимизации энергии. В общем случае задача минимизации является NP-трудной, поэтому зачастую получаемое решение является приближенным и может сильно различаться для разных алгоритмов.
- Вид графа G.
Остановимся подробнее на последнем критерии. Здесь важно выделить два принципиально разных случая. Если граф G содержит циклы, решение почти всегда может быть найдено лишь приближенно. Обычно в роли G в таком случае выступает граф изображения, а наиболее часто используемыми алгоритмами минимизации энергии являются метод на основе разрезов графов (graph cuts) [12], алгоритм TRW-S [13] и квадратичная псевдобулева оптимизация (QPBO) [14]. Например, алгоритм плотного стерео на основе разрезов графов был предложен в работе [15]. (Графом изображения, или графом-решеткой, будем называть граф, вершины которого соответствуют пикселям изображения, а ребра соединяют соседние вершины по принципу четырехсвязности.)
Если граф G не содержит циклов, то есть является деревом, становится возможным точное вычисление глобального минимума с помощью метода динамического программирования. По существу все методы данной подгруппы различаются лишь тем, какие из ребер графа-решетки они удаляют для устранения циклов. Несколько устаревшим является алгоритм scanline optimization [3], независимо оптимизирующий каждую строку изображения. Его характерным недостатком является рассогласованность диспаритетов соседних строк в итоговом решении (рис. 6б). Более современным и интересным в контексте данной работы подходом является алгоритм [16], использующий понятие минимального покрывающего дерева. Каждому ребру (p, q) исходного графа-решетки присваивается вес 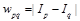 , после чего часть ребер удаляется таким образом, чтобы сумма весов оставшихся ребер была минимальна. В основе данной идеи лежит наблюдение о том, что области разрыва диспаритета, как правило, совпадают с краями на изображении. Таким образом, если два соседних пикселя имеют схожую яркость, то с большой вероятностью их диспаритеты равны или близки, а значит, ребро между соответствующими вершинами графа должно быть сохранено. В противном случае ребро можно удалить. При таком подходе значительно сокращается рассогласованность по строкам, однако появляются вертикально рассогласованные фрагменты (рис. 6в).
, после чего часть ребер удаляется таким образом, чтобы сумма весов оставшихся ребер была минимальна. В основе данной идеи лежит наблюдение о том, что области разрыва диспаритета, как правило, совпадают с краями на изображении. Таким образом, если два соседних пикселя имеют схожую яркость, то с большой вероятностью их диспаритеты равны или близки, а значит, ребро между соответствующими вершинами графа должно быть сохранено. В противном случае ребро можно удалить. При таком подходе значительно сокращается рассогласованность по строкам, однако появляются вертикально рассогласованные фрагменты (рис. 6в).
В целом глобальные алгоритмы обеспечивают немного более качественные результаты, чем локальные методы, но время их работы в среднем больше. Однако получаемые карты диспаритета все равно содержат ошибки. В первую очередь это обусловлено чересчур упрощенным характером оптимизируемых функций: закладываемые в них априорные предположения слишком просты и недостаточно отражают реалии нашего мира.
 Полуглобальные методы. В последние годы приобретают популярность алгоритмы, совмещающие черты локальных и глобальных методов. Подобно локальным методам они принимают решение в каждом пикселе независимо, однако подобно глобальным методам на это решение оказывают влияние пиксели, не ограниченные лишь локальной окрестностью данного: зачастую каждая точка изображения влияет на решение в любой другой точке.
Полуглобальные методы. В последние годы приобретают популярность алгоритмы, совмещающие черты локальных и глобальных методов. Подобно локальным методам они принимают решение в каждом пикселе независимо, однако подобно глобальным методам на это решение оказывают влияние пиксели, не ограниченные лишь локальной окрестностью данного: зачастую каждая точка изображения влияет на решение в любой другой точке.
Наиболее известным из методов данной группы является алгоритм SGM (Semi-Global Matching) [17]. Форма дерева в нем фиксируется заранее и представляет собой набор лучей, выходящих из одной точки. Такое дерево строится для каждого пикселя, и диспаритет в пикселе вычисляется путем динамического программирования по дереву. (Технически алгоритм реализован несколько иначе: решение в каждой точке получается в результате нескольких проходов по всем пикселям изображения вдоль направлений, задаваемых лучами дерева. Но это деталь реализации, не имеющая в данном контексте существенного значения.) В получаемых результатах отсутствует рассогласованность, однако возникают проблемы в слабо текстурированных областях. Это происходит в тех случаях, когда лучи, выходящие из точки, не покрывают достаточное количество текстуры. Заметим, что в самом названии алгоритма отражен его полуглобальный характер.
Развитием алгоритма SGM можно считать метод SimpleTree, предложенный в 2008 году в работе [18]. Алгоритм призван устранить упомянутый недостаток алгоритма SGM за счет включения в процесс оптимизации всех пикселей изображения. Для этого в каждой точке строятся два дерева специальной формы – горизонтально и вертикально ориентированные. Значение энергии, полученное при оптимизации методом динамического программирования по одному из деревьев, используется в качестве унарного потенциала при оптимизации по второму дереву. При этом форма деревьев позволяет эффективно реализовать вычисление диспаритетов в каждой точке.
Отметим еще один полуглобальный алгоритм, идейно отличающийся от двух уже рассмотренных и имеющий важное значение в контексте данной работы. Алгоритм был предложен Янгом в 2012 году [19] и является одним из новейших методов плотного стерео на текущий момент. Как и рассмотренный алгоритм из [16], метод Янга основан на использовании минимального покрывающего дерева, построенного для исходного графа-решетки, каждому ребру (p, q) которого присвоен вес 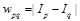 . Однако в отличие от уже рассмотренного метода алгоритм Янга не производит глобальную оптимизацию по полученному дереву, а работает подобно локальным алгоритмам с адаптивными весами, используя дерево для агрегации по нему стоимостей вместо стандартного окна. При этом вес пикселя q при вычислении решения в пикселе p зависит от расстояния Dpq, определяемого как сумма весов вдоль кратчайшего пути между соответствующими вершинами дерева. Таким образом, выражение для агрегированной стоимости присвоения диспаритета d пикселю q имеет вид
. Однако в отличие от уже рассмотренного метода алгоритм Янга не производит глобальную оптимизацию по полученному дереву, а работает подобно локальным алгоритмам с адаптивными весами, используя дерево для агрегации по нему стоимостей вместо стандартного окна. При этом вес пикселя q при вычислении решения в пикселе p зависит от расстояния Dpq, определяемого как сумма весов вдоль кратчайшего пути между соответствующими вершинами дерева. Таким образом, выражение для агрегированной стоимости присвоения диспаритета d пикселю q имеет вид
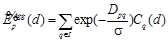 , (2)
, (2)
где I – данное изображение; Cq(d) – стоимость присвоения диспаритета d пикселю q; s – параметр алгоритма, влияющий на гладкость решения. Как и в локальных алгоритмах, в качестве решения в каждом пикселе выбирается диспаритет, дающий наименьшую агрегированную стоимость: 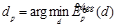 .
.
Достоинством метода Янга является высокая вычислительная эффективность, сопоставимая с эффективностью простейших локальных алгоритмов. В работе предложен быстрый способ вычисления агрегированных стоимостей в каждом пикселе изображения, требующий лишь два прохода по дереву. Однако недостатком алгоритма является неявное присвоение всем точкам изображения одного и того же значения диспаритета в процессе агрегации. Точки, между которыми существует путь в дереве без сильных перепадов яркости, оказывают сильное влияние друг на друга, и алгоритм способствует присвоению таким точкам одинаковых значений диспаритета. Другими словами, алгоритм поощряет наличие фронтально-параллельных плоскостей в итоговом решении, что зачастую не соответствует наблюдаемой реальной сцене. (Фронтально-параллельными (fronto-parallel) будем называть плоскости в трехмерной сцене, параллельные плоскости изображения. Очевидно, точки на такой плоскости имеют одинаковую глубину, поэтому в картах диспаритета им соответствуют области с постоянным значением диспаритета.)
 Проблема наклонных поверхностей. Алгоритмы на основе аппроксимации поверхностями. Проблема алгоритма Янга, упомянутая ранее, характерна для большинства методов, ищущих решение в пространстве диспаритетов. Если в сцене имеется поверхность с плавно изменяющейся глубиной (будем называть такие поверхности наклонными), то алгоритмам, не делающим никаких явных предположений о наличии таких поверхностей, крайне трудно правильно оценить подобные плавные изменения. Как правило, соответствующие участки получаемых карт диспаритета оказываются сегментироваными на несколько областей постоянного диспаритета с резкими переходами между ними (рис. 7).
Проблема наклонных поверхностей. Алгоритмы на основе аппроксимации поверхностями. Проблема алгоритма Янга, упомянутая ранее, характерна для большинства методов, ищущих решение в пространстве диспаритетов. Если в сцене имеется поверхность с плавно изменяющейся глубиной (будем называть такие поверхности наклонными), то алгоритмам, не делающим никаких явных предположений о наличии таких поверхностей, крайне трудно правильно оценить подобные плавные изменения. Как правило, соответствующие участки получаемых карт диспаритета оказываются сегментироваными на несколько областей постоянного диспаритета с резкими переходами между ними (рис. 7).
 Наличие большого числа наклонных поверхностей, в частности плоскостей, особенно характерно для сцен антропогенной природы, таких как уличные городские сцены, внутренние помещения, искусственно созданные объекты и т.д. Примеры подобных изображений приведены на рисунке 8.
Наличие большого числа наклонных поверхностей, в частности плоскостей, особенно характерно для сцен антропогенной природы, таких как уличные городские сцены, внутренние помещения, искусственно созданные объекты и т.д. Примеры подобных изображений приведены на рисунке 8.
Для решения данной проблемы уже предложено несколько подходов. Один из них основан на идее цветовой сегментации изображения и аппроксимации каждого сегмента некоторой поверхностью. Подобные алгоритмы состоят из двух основных шагов. На первом шаге с помощью одного из локальных алгоритмов вычисляется приближенное решение, полученная карта диспаритета используется для инициализации каждого цветового сегмента некоторой поверхностью (как правило, плоскостью). Таким образом, получается множество поверхностей, присутствующих в сцене. После этого на втором шаге производится разметка сегментов поверхностями из полученного множества с помощью одного из алгоритмов глобальной оптимизации, например метода разрезов графа. Описанной схеме следуют, например, алгоритмы из работ [20, 21].
В работе [22] набор поверхностей не фиксируется на этапе инициализации, а уточняется в процессе разметки. Также представляет интерес алгоритм [23], в котором цветовая сегментация не является жестким ограничением: отнесение двух пикселей одного сегмента к одной поверхности поощряется, но необязательно. Особенностью этой работы является и то, что тип поверхностей не ограничен только плоскостями, а рассматриваются и более общие B-сплайны.
К числу достоинств методов на основе сегментации стоит отнести относительно высокую надежность в слабо текстурированных областях, а также возможность восстанавливать достоверные значения диспаритета в областях перекрытия: если часть сегмента принадлежит области перекрытия, но самому сегменту присвоена правильная поверхность, то и диспаритет в загороженных пикселях будет верным.
Заметно выделяется среди прочих предложенный в 2011 году алгоритм PatchMatch [24]. Он не использует цветовую сегментацию и производит попиксельную разметку изображения, однако в качестве меток используются не значения диспаритета, а плоскости в пространстве {x, y, d}. Использование плоскостей позволяет получать дробные значения диспаритетов, что важно для областей, где глубина изменяется очень плавно. Начальная плоскость в каждом пикселе генерируется случайным образом, после чего запускается итеративная процедура уточнения плоскостей по всему изображению. При этом происходит распространение хороших плоскостей от пикселя к пикселю. При вычислении стоимости присвоения плоскости некоторому пикселю его окрестность как бы проецируется на данную плоскость, избегая тем самым неявного предположения о константности диспаритета внутри окна, характерного для локальных алгоритмов.
Одним из главных недостатков рассмотренных алгоритмов на основе аппроксимации плоскостями является низкая скорость работы. Если используется цветовая сегментация, то, как правило, именно она является узким местом алгоритма в плане его вычислительной эффективности. Алгоритм PatchMatch, хотя и не использует сегментацию, но также является медленным: в авторской реализации время его работы на изображении размером 0,1 мегапикселя составляет около 1 минуты.
Выводы. Проведенный обзор показывает, что задача плотной стереореконструкции по паре изображений на сегодняшний день не решена. Известные алгоритмы обеспечивают либо высокую скорость работы, либо хорошее качество, но не то и другое одновременно. При этом существует ряд характерных трудностей, на которые приходится наибольшее количество ошибок в результатах. К их числу можно отнести области перекрытия, слабо текстурированные зоны и наклонные поверхности с плавным изменением диспаритета. Первая из них неизбежна практически при любых входных данных, а последние две особенно часто встречаются в реальных практических задачах, когда исходными данными являются уличные сцены или изображения внутренних помещений. Основными поверхностями в таком случае выступают плоскость дороги, плоскости стен зданий, потолков и т.д. Все они, как правило, не обладают ярко выраженной текстурой. А общий недостаток существующих сегодня алгоритмов на основе аппроксимации сцены поверхностями – медленная скорость работы.
Предлагаемый алгоритм
В данной работе предлагается новый алгоритм плотного стерео, нацеленный на работу с изображениями сцен, содержащих значительное число наклонных плоскостей. Как и методы, рассмотренные выше, предлагаемый алгоритм работает не в пространстве диспаритетов. Но при этом он не использует цветовую сегментацию и в отличие от алгоритма PatchMatch оперирует конечным набором заранее вычисленных плоскостей, что позволяет организовать быструю разметку изображения. Общую схему алгоритма можно представить в виде следующих шагов.
- Нахождение множества контрольных точек путем сопоставления ректифицированных изображений.
- Вычисление набора плоскостей-гипотез при помощи полученного множества контрольных точек.
- Разметка изображения плоскостями из вычисленного набора.
Рассмотрим каждый из этих шагов.
Нахождение множества контрольных точек. Контрольными точками (Ground Control Points, GCP) в контексте задачи плотного стерео называют разреженное множество точек, значение диспаритета в которых известно достоверно либо с высокой степенью уверенности. В ряде практических сценариев множество контрольных точек может быть дано на входе алгоритма. Например, оно может быть получено из этапа сопоставления изображений, предшествующего ректификации снимков: полученные в процессе сопоставления пары характерных точек являются достаточно надежными. Также в качестве контрольных точек могут использоваться данные лазерного сканирования, если они имеются. В случае, когда контрольные точки неизвестны заранее, они могут быть получены непосредственно из пары ректифицированных изображений. Так, в статье [25] в качестве контрольных предлагается использовать точки, в которых три разных локальных алгоритма дали одинаковый диспаритет.
 В данной работе множество контрольных точек GCP получалось путем сопоставления ректифицированных изображений. Использовалась стандартная схема сопоставления изображений на основе особых точек и алгоритма RANSAC [26]. В качестве дополнительной проверки использовалось условие принадлежности пары сопоставленных точек одной строке изображения. Для поиска и сравнения характерных точек применялись детектор Харриса [27] и дескриптор SIFT [28]. На рисунке 9 приведен пример множества контрольных точек, вычисленных для одного из тестовых изображений.
В данной работе множество контрольных точек GCP получалось путем сопоставления ректифицированных изображений. Использовалась стандартная схема сопоставления изображений на основе особых точек и алгоритма RANSAC [26]. В качестве дополнительной проверки использовалось условие принадлежности пары сопоставленных точек одной строке изображения. Для поиска и сравнения характерных точек применялись детектор Харриса [27] и дескриптор SIFT [28]. На рисунке 9 приведен пример множества контрольных точек, вычисленных для одного из тестовых изображений.
Вычисление набора плоскостей-гипотез. Одна из ключевых проблем, связанных с переходом из пространства диспаритетов в пространство плоскостей, – это получение набора плоскостей F, из которых будет делаться выбор в каждом пикселе. Чтобы решение было качественным, этот набор не должен быть слишком большим, но в то же время должен содержать все основные плоскости, присутствующие в сцене. Для вычисления F предлагается использовать полученное на первом шаге множество контрольных точек GCP.
 Заметим, что множество GCP фактически представляет собой облако трехмерных точек в пространстве {x, y, d}, поэтому задачу вычисления набора плоскостей F можно сформулировать как задачу сегментации облака трехмерных точек на плоскости. Для этого в данной работе применяется жадный алгоритм, состоящий из следующих шагов.
Заметим, что множество GCP фактически представляет собой облако трехмерных точек в пространстве {x, y, d}, поэтому задачу вычисления набора плоскостей F можно сформулировать как задачу сегментации облака трехмерных точек на плоскости. Для этого в данной работе применяется жадный алгоритм, состоящий из следующих шагов.
- Вычисление алгоритмом RANSAC параметров плоскости, поддерживаемой наибольшим числом точек из GCP. Добавление плоскости в множество F.
- Исключение поддерживающих плоскость точек из множества GCP.
- Повторение шагов 1 и 2, пока существуют плоскости, поддерживаемые достаточным числом точек. Количество точек, поддержка которых необходима для включения плоскости в набор, является параметром алгоритма.
Алгоритм позволяет надежно вычислить основные плоскости сцены. В случае наземной городской съемки, как на рисунке 9, это в первую очередь плоскости земли и стен зданий. Они, как правило, находятся первыми. Однако на поздних итерациях после исключения большей части точек возможна сегментация и менее значимых плоскостей.
Выбор оптимальной плоскости в каждой точке. На заключительном шаге каждому пикселю p изображения присваивается некоторая плоскость fÎF. Пусть 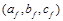 – параметры плоскости f. Тогда значение диспаритета в точке p будем вычислять по формуле
– параметры плоскости f. Тогда значение диспаритета в точке p будем вычислять по формуле
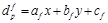 . (3)
. (3)
Данное выражение для диспаритета уже встречалось, например, в работе [24].
Для вычисления стоимости присвоения плоскости f пикселю p используется следующее выражение:
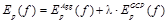 . (4)
. (4)
Здесь величина 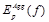 отражает стоимость присвоения плоскости f точке p, агрегированную по всем пикселям изображения, а
отражает стоимость присвоения плоскости f точке p, агрегированную по всем пикселям изображения, а 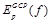 представляет собой штраф за отклонение от регуляризирующего решения DGCP, полученного с использованием только контрольных точек.
представляет собой штраф за отклонение от регуляризирующего решения DGCP, полученного с использованием только контрольных точек.
Для вычисления стоимости 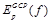 используется подход, предложенный Янгом [19]. Пусть T – минимальное покрывающее дерево, построенное для исходного графа-решетки изображения IL, вес ребра (p, q) в котором равен разности яркости соответствующих пикселей:
используется подход, предложенный Янгом [19]. Пусть T – минимальное покрывающее дерево, построенное для исходного графа-решетки изображения IL, вес ребра (p, q) в котором равен разности яркости соответствующих пикселей: 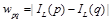 . Пусть Dpq – сумма весов ребер вдоль кратчайшего пути между точками p и q в дереве T. Тогда по аналогии с формулой (2) получим:
. Пусть Dpq – сумма весов ребер вдоль кратчайшего пути между точками p и q в дереве T. Тогда по аналогии с формулой (2) получим:
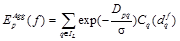 , (5)
, (5)
где 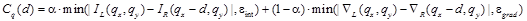 . (6)
. (6)
Здесь 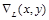 и
и 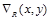 – величины градиента в пикселе (x, y) левого и правого изображений соответственно,
– величины градиента в пикселе (x, y) левого и правого изображений соответственно, 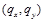 – координаты пикселя
– координаты пикселя 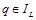 ,
, 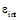 и
и 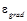 – пороги, а a – коэффициент, определяющий степень влияния яркостной и градиентной составляющих.
– пороги, а a – коэффициент, определяющий степень влияния яркостной и градиентной составляющих.
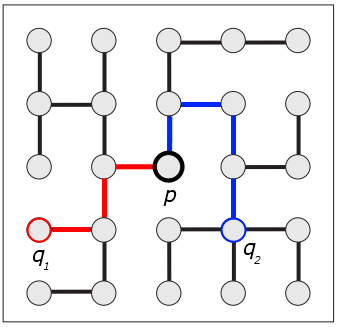
Принцип агрегации стоимостей по дереву проиллюстрирован на рисунке 10. Каждый пиксель qi изображения вносит свой вклад, зависящий от расстояния между соответствующими вершинами на дереве. Поскольку вес ребра равен разности яркости между соседними пикселями, небольшие расстояния на дереве будут характерны для тех точек, между которыми существует путь без существенных перепадов яркости на изображении. (Строго говоря, это не совсем так, поскольку из-за отсутствия в дереве части ребер исходного графа-решетки не для каждого пути между пикселями изображения существует соответствующий путь в дереве. Но так как при построении минимального покрывающего дерева в первую очередь отбрасываются ребра с большими перепадами яркости, пути малой стоимости существуют в дереве в большинстве случаев.) Таким образом, точки из одного цветового сегмента на изображении будут оказывать друг на друга сильное влияние, а пиксели, разделенные цветовой границей, значительно меньшее.
В каком-то смысле такой подход можно считать аналогом идеи об уменьшении веса пикселей, разделенных цветовыми границами, предложенной в более ранней работе [10]. Однако в данном случае влияние пикселей не ограничено локальной окрестностью. Также данный подход можно сравнить с подходами на основе цветовой сегментации, но ключевое отличие заключается в том, что сегменты не фиксируются жестким образом.
Отметим еще раз, что описанный подход был впервые применен в алгоритме Янга, однако в нем агрегация по дереву производилась для постоянного значения диспаритета. В предложенном алгоритме диспаритет 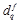 в каждой точке может быть разным и зависит от плоскости f, для которой проводится агрегация. Это позволяет относить связные однотонные области на изображении не только к фронтально-параллельным, но и к произвольным наклонным плоскостям. Можно сказать, что алгоритм Янга является частным случаем предложенного метода, когда набор F состоит исключительно из фронтально-параллельных плоскостей, глубина которых в сцене соответствует значениям диспаритета {dmin, dmin+1, …, dmax}.
в каждой точке может быть разным и зависит от плоскости f, для которой проводится агрегация. Это позволяет относить связные однотонные области на изображении не только к фронтально-параллельным, но и к произвольным наклонным плоскостям. Можно сказать, что алгоритм Янга является частным случаем предложенного метода, когда набор F состоит исключительно из фронтально-параллельных плоскостей, глубина которых в сцене соответствует значениям диспаритета {dmin, dmin+1, …, dmax}.
Одной из особенностей агрегации точек для произвольной наклонной плоскости f является то, что почти всегда существуют точки q, для которых 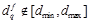 . Такая ситуация требует специальной обработки, поскольку выход за пределы диапазона значений диспаритета считается невозможным. Одним из вариантов было бы исключение подобных точек из процесса агрегации и усреднение величины
. Такая ситуация требует специальной обработки, поскольку выход за пределы диапазона значений диспаритета считается невозможным. Одним из вариантов было бы исключение подобных точек из процесса агрегации и усреднение величины 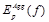 по количеству точек с корректным значением диспаритета. Однако в таком случае возникает проблема вырожденных плоскостей, для которых лишь несколько точек оказываются правильными. В данной работе использовался другой подход: за выход за пределы допустимого диапазона на точку накладывался достаточно большой штраф
по количеству точек с корректным значением диспаритета. Однако в таком случае возникает проблема вырожденных плоскостей, для которых лишь несколько точек оказываются правильными. В данной работе использовался другой подход: за выход за пределы допустимого диапазона на точку накладывался достаточно большой штраф 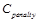 , одинаковый для всех точек.
, одинаковый для всех точек.
Рассмотрим теперь принцип вычисления второго слагаемого из формулы (4), 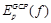 . Поскольку для контрольных точек с высокой степенью надежности известны правильные значения диспаритета, представляется естественным использовать их не только для вычисления набора плоскостей F, но и для регуляризации решения, придания ему дополнительной гладкости. Для этого предлагается следующий подход.
. Поскольку для контрольных точек с высокой степенью надежности известны правильные значения диспаритета, представляется естественным использовать их не только для вычисления набора плоскостей F, но и для регуляризации решения, придания ему дополнительной гладкости. Для этого предлагается следующий подход.
- Вычислить регуляризирующее решение DGCP с использованием только контрольных точек.
- Функцию
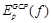 определить таким образом, чтобы за отклонение итогового решения от DGCP в каждой точке накладывался штраф.
определить таким образом, чтобы за отклонение итогового решения от DGCP в каждой точке накладывался штраф.
Идея вычислять регуляризирующую карту диспаритета DGCP для всего изображения обусловлена следующими соображениями. В случае, когда плоскость сцены обладает достаточной текстурой, точки данной плоскости на изображении зачастую оказываются отделенными друг от друга сильными перепадами яркости и, как следствие, оказывают друг на друга слабое влияние. Решение в каждом пикселе начинает сильнее зависеть от точек с похожей яркостью из ближайшей локальной окрестности, что приводит к характерным ошибкам: на карте диспаритета появляются отдельные сегменты, являющиеся частью некоторого большого плоского участка, но отнесенные при этом к неправильным плоскостям.
При вычислении DGCP только на основе контрольных точек пиксели из локальных окрестностей, не являющиеся контрольными, перестают оказывать какое-либо влияние. В результате начинает распространяться та плоскость, которая наилучшим образом вписывается в контрольные точки. В случае больших плоских участков сцены это почти всегда оказывается правильная плоскость. Наложение дополнительного штрафа за отклонение итогового решения от DGCP позволяет избежать указанной проблемы с отдельными ошибочными сегментами внутри больших плоских областей.
Для вычисления DGCP возьмем уже имеющееся минимальное покрывающее дерево T и будем производить по нему агрегацию согласно формуле (5), но с измененным выражением стоимости за присвоение диспаритета d пикселю q:
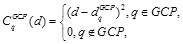 (7)
(7)
где 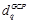 – значение диспаритета в контрольной точке q.
– значение диспаритета в контрольной точке q.
Соответственно, выражение для агрегированной стоимости примет вид:
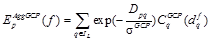 . (8)
. (8)
Пусть 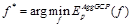 – плоскость, обладающая наименьшей стоимостью в точке p. Тогда значение регуляризирующей карты диспаритета DGCP в данной точке может быть вычислено из уравнения этой плоскости:
– плоскость, обладающая наименьшей стоимостью в точке p. Тогда значение регуляризирующей карты диспаритета DGCP в данной точке может быть вычислено из уравнения этой плоскости: 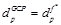 .
.
Стоит отметить, что подобный способ вычисления регуляризирующей карты диспаритета похож на метод постобработки, использующийся в алгоритме Янга. В нем надежными считаются точки, прошедшие проверку на консистентность между картами диспаритета для левого и правого изображений, а значения диспаритета в них – выбранные в результате агрегации по минимальному покрывающему дереву. (Стандартная проверка, используемая многими алгоритмами плотного стерео с целью выявления ненадежных точек, в частности областей перекрытия. В англоязычной литературе называется left-right consistency check. Пусть d – вычисленная величина диспаритета в точке (x, y)ÎIL. Проверка считается пройденной для данной точки, если диспаритет точки (x–d, y)ÎIR также равен d, то есть соответствующие точки на обоих изображениях переходят друг в друга.) Однако в данном случае преследуется иная цель, нежели улучшение готового решения. Также в силу большей надежности контрольных точек введена квадратичная зависимость штрафа от отклонения диспаритета от правильного значения (формула (7)).
Имея регуляризирующее решение DGCP, полученное описанным выше способом, определим штраф за отклонение от него итогового решения следующим образом:
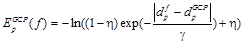 , (9)
, (9)
где h и g – параметры функции. Данный вид штрафной функции в применении к задаче плотной стереореконструкции был предложен в работе [25], авторы которой включили ее в качестве третьего слагаемого в общий функционал энергии. Однако алгоритм из [25], хотя и работает также с контрольными точками, но принципиально отличается от предложенного в данной работе: метод является глобальным и использует алгоритм разрезов графа для поиска оптимальной разметки диспаритетами одновременно по всему изображению.
Как уже говорилось, итоговая стоимость присвоения плоскости f пикселю p вычисляется по формуле (4). В ней параметр l регулирует степень влияния карты диспаритета DGCP на итоговое решение.
Экспериментальная оценка
Выбор тестовой базы. Развитие многих задач компьютерного зрения, особенно давно известных и хорошо изученных, неразрывно связано с развитием соответствующих тестовых баз, используемых для оценки и сравнения алгоритмов. Для задачи плотного стерео главной и фактически единственной такой базой на протяжении последних десяти лет являлась база Middlebury [29], созданная в 2001 году [3] и расширявшаяся до 2006 года [30–32]. Создание этой базы наряду с предложенными в работе [3] систематизацией понятий и таксономией послужили сильным толчком для появления новых алгоритмов и развития данной области. Разработанная площадка для сравнения методов [33], организованная в форме рейтинга, собрала в одном месте большую часть всех существующих работ по данной теме и позволила исследователям наглядно оценивать сильные и слабые стороны тех или иных алгоритмов. По состоянию на 9 ноября 2012 года в рейтинге представлены 137 методов.
Однако у базы Middlebury есть недостатки. Во-первых, в наиболее полной версии она состоит из 38 пар изображений, что представляется недостаточным. Во-вторых, рейтинг алгоритмов составляется на основании их результатов на всего лишь 4 тестовых парах, что безусловно очень мало и не отражает всей полноты достоинств и недостатков алгоритмов. Наконец, в-третьих, все тестовые наборы были получены в лабораторных условиях и потому заметно отличаются от тех данных, с которыми приходится иметь дело в реальных практических задачах. Примеры изображений из набора Middlebury приведены на рисунке 11, а также уже встречались выше на рисунках 2, 6 и 7.
 Как следствие указанных недостатков многим алгоритмам характерно переобучение на изображениях из набора Middlebury. Методы, занимающие высокие позиции в рейтинге, зачастую оказываются непригодными для реальных практических задач. Авторы некоторых алгоритмов приводят результаты тестирования на других данных, однако они являются закрытыми и потому сравнение на них невозможно. Так, например, метод из [17] применялся к данным аэрофотосъемки.
Как следствие указанных недостатков многим алгоритмам характерно переобучение на изображениях из набора Middlebury. Методы, занимающие высокие позиции в рейтинге, зачастую оказываются непригодными для реальных практических задач. Авторы некоторых алгоритмов приводят результаты тестирования на других данных, однако они являются закрытыми и потому сравнение на них невозможно. Так, например, метод из [17] применялся к данным аэрофотосъемки.
Ввиду указанных причин для тестирования предложенного в рамках данной работы алгоритма было решено использовать другую тестовую базу, а именно базу KITTI (Karlsruhe Institute of Technology and Toyota Technological Institute) [34, 35], созданную и опубликованную в 2012 году. Этот тестовый набор был получен путем съемки со специального автомобиля, оборудованного камерами, лазерным сканером и датчиком GPS. Набор состоит из 778 пар ректифицированных изображений уличной городской съемки, для 194 из которых доступны эталонные данные. Размер каждого изображения составляет 1226×370 пикселей, то есть примерно 0,45 мегапикселя.
По сравнению с набором Middlebury набор KITTI содержит более интересные и сложные данные, представляющие практический интерес. При этом характер представленных в наборе сцен, содержащих значительное число наклонный плоскостей (поверхность дороги, стены зданий), позволяет наглядно продемонстрировать преимущества предложенного алгоритма.
Результаты на базе KITTI. Было проведено экспериментальное сравнение разработанного алгоритма с алгоритмом Янга [19], сопоставимым с ним по скорости работы. Использовались следующие представленные ранее значения параметров предложенного алгоритма: количество точек, поддержка которых необходима для включения плоскости в набор F, равнялось 10; l=40; s=sGCP=0,1; a=0,11; eint=7; egrad=2; Cpenalty=100; h=0,005; g=2.
Качество работы алгоритмов оценивалось по следующему критерию. Пусть d * – эталонное значение диспаритета в пикселе p; d – вычисленное значение диспаритета в этом же пикселе. Решение в точке p считается найденным правильно, если ½d – d *½<t, где t – порог, задающий максимально допустимое отклонение диспаритета от эталонного значения. Метрикой качества карты диспаритета D, полученной для изображения I, является доля пикселей, в которых было найдено верное решение. Пиксели, для которых эталонное значение диспаритета неизвестно, не учитываются. Данная метрика является стандартной для задачи плотного стерео и применяется, например, для ранжирования алгоритмов в рейтинге Middlebury. В экспериментах в рамках данной работы использовалось значение порога t=3.
Для сравнения алгоритмов использована выборка из базы KITTI, содержащая 194 пары изображений с известными эталонными картами диспаритета. Эти карты были получены путем лазерного сканирования и потому являются разреженными. В таблице указаны средняя, минимальная и максимальная ошибки по всей выборке для алгоритма Янга и для предложенного метода.
Результаты сравнения алгоритмов
|
Алгоритм |
Ошибка, % |
||
|
Средняя |
Минимальная |
Максимальная |
|
|
Янга |
33,03 |
8,82 |
73,46 |
|
Предложенный |
18,60 |
1,01 |
68,97 |
Как видно из таблицы, предложенный алгоритм превзошел метод Янга по доле пикселей с правильно вычисленным диспаритетом. Время работы алгоритма Янга составило примерно 1,5 секунды на стереопару, а предложенного алгоритма – около 5 секунд на стереопару. Время, необходимое для вычисления множества контрольных точек, не учитывалось, поскольку, как обсуждалось выше, во многих практических сценариях, включая задачу трехмерной реконструкции в общей постановке, их можно считать частью входных данных алгоритма. Тесты проводились на компьютере с процессором Intel Core i7-3770K, 3,50 ГГц.
Примеры работы алгоритмов приведены на рисунках 12 и 13. Видно, что метод Янга склонен к ошибочной сегментации решения на множество фронтально-параллельных плоскостей, или, другими словами, регионов с постоянным значением диспаритета. Предложенный алгоритм лишен этого недостатка и обеспечивает значительно более гладкое решение.

Таким образом, в данной работе был проведен обзор существующих методов плотной стереореконструкции по паре изображений и описан новый алгоритм. Как следует из обзора, существующие на сегодняшний день алгоритмы не способны обеспечить быстрый и качественный результат на различных типах входных данных. Так, одной из трудностей для большинства методов является наличие в сцене наклонных поверхностей с плавно изменяющимся вдоль них диспаритетом. Методы, явным образом нацеленные на решение данной проблемы, используют либо цветовую сегментацию, либо итеративную процедуру уточнения и распространения плоскостей от пикселя к пикселю (алгоритм PatchMatch). В обоих случаях это приводит к низкой скорости работы метода.
Как и алгоритм PatchMatch, предложенный метод присваивает каждому пикселю изображения определенную плоскость, исходя из которой вычисляется значение диспаритета. Однако предложенный метод использует конечный набор плоскостей, аппроксимирующих сцену. Для вычисления данного набора предлагается использовать контрольные точки. Во многих практических сценариях контрольные точки можно считать частью входных данных алгоритма, в противном случае они могут быть получены путем сопоставления ректифицированных изображений. Для вычисления набора плоскостей по контрольным точкам используется представление множества контрольных точек в виде облака трехмерных точек и применяется жадный алгоритм сегментации облака на плоскости.
Выбор оптимальной плоскости в каждом пикселе производится с помощью процедуры агрегации стоимостей по минимальному покрывающему дереву, предложенной в алгоритме Янга. Однако в отличие от алгоритма Янга агрегация происходит в пространстве плоскостей, а не диспаритетов. Для придания решению дополнительной гладкости и надежности предлагается подход, при котором по контрольным точкам вычисляется регуляризирующая карта диспаритета и за отклонение от нее в процессе вычисления итогового решения накладывается дополнительный штраф.
Приведены результаты экспериментальной оценки предложенного алгоритма в сравнении с сопоставимым с ним по скорости работы алгоритмом Янга. Эксперименты проводились на опубликованной в 2012 году тестовой базе KITTI, содержащей несколько сотен пар ректифицированных изображений наземной городской съемки. Показано, что предложенный алгоритм лишен характерного недостатка, проявляющегося в сегментации сцены на множество фронтально-параллельных плоских областей. Это подтверждается и численными результатами: ошибка, измеряемая долей пикселей с неправильно вычисленным диспаритетом, у предложенного алгоритма меньше.
Отметим также, что главным ограничением предложенного алгоритма является аппроксимация всей сцены множеством плоскостей, что неизбежно порождает ошибки на менее структурированных объектах естественной природы, таких как деревья, а также на неплоских объектах. В последнем случае решением могло бы стать расширение алгоритма на различные классы поверхностей. Сопутствующие проблемы может породить шаг вычисления набора плоскостей, которыми будет аппроксимироваться сцена. Неточная оценка параметров плоскостей, нахождение лишних или, наоборот, пропуск плоскостей, присутствующих в сцене, может привести к ошибкам в карте диспаритета. Для повышения надежности данного шага можно было бы дополнять множество контрольных точек другими примитивами, сопоставленными на двух изображениях, например, отрезками. Также кажется перспективным использование алгоритмов геометрического разбора изображений, например из работы [36].
Литература
- Вежневец B. Задача восстановления формы объекта по закраске (shape from shading) // Компьютерная графика и мультимедиа. 2004. URL: http://cgm.computergraphics.ru/content/view/59 (дата обращения: 9.11.2012).
- Hartley R., Zisserman A. Multiple View Geometry in Computer Vision. 2nd ed. Cambridge University Press, 2004.
- Scharstein D., Szeliski R. A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms, Intern. Journ. of Computer Vision, 2001, Vol. 47, pp. 7–42.
- Bleyer M., Chambon S. Does Color Really Help in Dense Stereo Matching? Intern. Symposium on 3D Data Processing, Visualization and Transmission, 2010, pp. 1–8.
- Birchfield S., Tomasi C. A Pixel Dissimilarity Measure That Is Insensitive to Image Sampling, IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, Vol. 20, pp. 401–406.
- Mühlmann K., Maier D., Hesser J., Männer R. Calculating Dense Disparity Maps from Color Stereo Images, an Efficient Implementation, Intern. Journ. of Computer Vision, 2001, Vol. 47, pp. 79–88.
- Fusiello A., Roberto V., Trucco E. Efficient Stereo with Multiple Windowing, IEEE Conf. on Computer Vision and Pattern Recognition, 1997, pp. 858–863.
- Hirschmüller H., Innocent P.R., Garibaldi J. Real-Time Correlation-Based Stereo Vision with Reduced Border Errors, Intern. Journ. of Computer Vision, 2002, Vol. 47, no. 1–3, pp. 229–246.
- Yoon K.-J., Kweon I.-S. Adaptive Support-Weight Approach for Correspondence Search, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, Vol. 28, no. 4, pp. 650–656.
- Hosni A., Bleyer M., Gelautz M., Rhemann C. Local Stereo Matching Using Geodesic Support Weights, IEEE Intern. Conf. on Image Processing, 2009, pp. 2093–2096.
- Tappen M.F., Freeman W.T. Comparison of Graph Cuts with Belief Propagation for Stereo, using Identical MRF Parameters, Intern. Conf. on Computer Vision, 2003, pp. 900–907.
- Y., Veksler O., Zabih R. Fast Approximate Energy Minimization via Graph Cuts, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, Vol. 23, no. 11, pp. 1222–1239.
- Kolmogorov V. Convergent Tree-Reweighted Message Passing for Energy Minimization, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, Vol. 28, no. 10, pp. 1568–1583.
- Kolmogorov V., Rother C. Minimizing Nonsubmodular Functions with Graph Cuts – A Review, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, Vol. 29, no. 7, pp. 1274–1279.
- Kolmogorov V., Zabih R. Computing Visual Correspondence with Occlusions via Graph Cuts, Intern. Conf. on Computer Vision, 2001, pp. 508–515.
- Veksler O. Stereo Correspondence by Dynamic Programming on a Tree, IEEE Conf. on Computer Vision and Pattern Recognition, 2005, pp. 384–390.
- Hirschmüller H. Stereo Processing by Semiglobal Matching and Mutual Information, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, Vol. 30, no. 2, pp. 328–341.
- Bleyer M., Gelautz M. Simple but Effective Tree Structures for Dynamic Programming-Based Stereo Matching, Intern. Conf. on Computer Vision Theory and Applications, 2008, pp. 415–422.
- Yang Q. A Non-Local Cost Aggregation Method for Stereo Matching, IEEE Conf. on Computer Vision and Pattern Recognition, 2012, pp. 1402–1409.
- Bleyer M., Gelautz M. A Layered Stereo Algorithm Using Image Segmentation and Global Visibility Constraints, IEEE Intern. Conf. on Image Processing, 2004, pp. 2997–3000.
- Klaus A., Sormann M., Karner K. Segment-Based Stereo Matching Using Belief Propagation and a Self-Adapting Dissimilarity Measure, Intern. Conf. on Pattern Recognition, Vol. 3, 2006, pp. 15–18.
- Wang Z.-F., Zheng Z.-G. A Region Based Stereo Matching Algorithm Using Cooperative Optimization, IEEE Conf. on Computer Vision and Pattern Recognition, 2008.
- Bleyer M., Rother C., Kohli P. Surface Stereo with Soft Segmentation, IEEE Conf. on Computer Vision and Pattern Recognition, 2010, pp. 1570–1577.
- Bleyer M., Rhemann C., Rother C. PatchMatch Stereo – Stereo Matching with Slanted Support Windows, British Machine Vision Conf., 2011, pp. 14.1–14.11.
- Wang L., Yang R. Global Stereo Matching Leveraged by Sparse Ground Control Points, IEEE Conf. on Computer Vision and Pattern Recognition, 2011, pp. 3033–3040.
- Fischler M.A., Bolles R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography, Communications of the ACM, 1981, Vol. 24, no. 6, pp. 381–395.
- Harris C., Stephens M. A Combined Corner and Edge Detector, Fourth Alvey Vision Conference, 1988, pp. 147–151.
- Lowe D.G. Distinctive Image Features from Scale-Invariant Keypoints, Intern. Journ. of Computer Vision, 2004, Vol. 60, no. 2, pp. 91–110.
- Middlebury Stereo Datasets. URL: http://vision.middlebury.edu/stereo/data/ (дата обращения: 9.11.2012).
- Scharstein D., Szeliski R. High-Accuracy Stereo Depth Maps Using Structured Light, IEEE Conf. on Computer Vision and Pattern Recognition, 2003, pp. 195–202.
- Scharstein D., Pal C. Learning Conditional Random Fields for Stereo, IEEE Conf. on Computer Vision and Pattern Recognition, 2007, pp. 1–8.
- Hirschmüller H., Scharstein D. Evaluation of Cost Functions for Stereo Matching, IEEE Conf. on Computer Vision and Pattern Recognition, 2007, pp. 1–8.
- Middlebury Stereo Evaluation – Version 2. URL: http://vision.middlebury.edu/stereo/eval/ (дата обращения: 9.11.2012).
- Karlsruhe Institute of Technology and Toyota Technological Institute Stereo Evaluation Dataset. URL: http://www.cvlibs.net/datasets/kitti/eval_stereo_flow.php?benchmark=stereo (дата обращения: 9.11.2012).
- Geiger A., Lenz P., Urtasun R. Are We Ready for Autonomous Driving? The KITTI Vision Benchmark Suite, IEEE Conf. on Computer Vision and Pattern Recognition, 2012, pp. 3354–3361.
- Tretyak E., Barinova O., Kohli P., Lempitsky V. Geometric Image Parsing in Man-Made Environment, Intern. Journ. of Computer Vision, 2012, Vol. 97, no. 3, pp. 305–321.
Comments